Las distribuciones de probabilidad permiten explicar muchos fenómenos reales que causan incertidumbre. En este artículo se abordará la Distribución Normal, una de las distribuciones de probabilidad más comunes y que es utilizada en diversos de contextos, si alguna vez estudias algo de estadística es posible que te topes con está distribución.
Algo de historia sobre la distribución normal
La distribución normal (aunque todavía no con ese nombre) apareció por primera vez en 1733, en la obra del matemático inglés Abraham de Moivre. De Moivre descubrió que la forma limitante de la distribución binomial (discreta), cuando el número de pruebas del experimento binomial se convierte en infinitamente grande, es la función de densidad de probabilidad que hoy llamamos la distribución normal (continua).
Stigler (1986), transmite, con cierto detalle analítico, la satisfacción de Moivre por el descubrimiento que tanto le costó conseguir.
En un libro sobre el movimiento planetario, publicado en 1809, el matemático Alemán Carl Friedrich Gauss presentó su trabajo pionero sobre el método de estimación por mínimos cuadrados. Fue en este contexto que propuso la distribución normal como un buen modelo teórico para la distribución probabilística de los errores de medición aleatorios del mundo real.
Otro matemático francés, Pierre Simon Laplace, trabajó en está distribución. A principios de 1810 presentó su primera demostración de lo que hoy conocemos (de forma más general) como el Teorema del Límite Central.
Por otro lado, los matemáticos del siglo XIX llamarón a la distribución Normal la distribución de Gauss-Laplace. Sin embargo, con el paso del tiempo, este nombre dio paso a la distribución gaussiana.
Otro aspecto curioso es que el nombre de «normal» para esta distribución, apareció por primera vez cuando Francis Galton la dio a conocer a un amplio público en su libro de 1889 Natural Inheritance.
Usos de la Distribución Normal
El argumento más teórico para el uso de la distribución Normal son los Teoremas del Límite Central, aunque muchas otras distribuciones de frecuencias pueden también aproximarse a esta distribución. Además, la distribución normal es importante en la Inferencia Estadística y en el análisis de datos, dado que muchas de las estadísticas muestrales tienden a una distribución Normal en la misma medida con la cual crece el tamaño de las muestras.
Esta distribución tiene la propiedad de adaptarse a las distribuciones observadas de frecuencias en muchos fénomenos.
Definición Matemática
Sea
una variable aleatoria con distribución de probabilidad normal, entonces
La función de distribución de probabilidad (pdf):
donde los parámetros son
y
.
La función generatriz de momentos:
Media
Varianza
Características del gráfico de la curva Normal
- Tiene forma acampanada.
- Es simétrico con respecto a la media
. Es unimodal, por tanto la media, la moda y la mediana coinciden. - Los extremos de la curva se aproximan al eje horizontal pero nunca llegan a cortarlo. Esto indica que el eje x es asíntota por la derecha y la izquierda de f(x).
- El área total de la curva es 1.
- Su forma puede ser más puntiaguda o aplanada dependiendo de la varianza.
Hagamos cálculos asociados a la Distribución Normal con Python
En esta ocasión usaremos el submódulo del paquete científico Scipy específicamente norm. Como instancia de la clase rv_continuous, el objeto norm hereda de ella una colección de métodos genéricos y los completa con detalles específicos para esta distribución en particular.
La palabra clave ubicación (loc) especifica la media. La palabra clave escala (scale) especifica la desviación estándar.

Ejemplos de aplicación de los métodos
Ejemplo 1.
La variable aleatoria
representa una medida de la inteligencia mediante pruebas que se aplican en la determinación del coeftciente intelectual (CI). Si
está distribuida normal con media 100 y desviación 10. Calcular:
- La probabilidad de que X sea mayor que 100.
- La probabilidad de que X sea menor que 85.
- La probabilidad de que X sea a lo sumo 112.
- La probabilidad de que X sea al menos 108.
- La probabilidad de que X sea mayor que 90.
- La probabilidad de que se encuentre entre 95 y 120.
Para todos los casos pasamos una distribución normal N (0,1), mediante el cambio X- X-100 10 Z = à, Queremos calcular P (X> 100) = 1- P (X <100) = 1-P (z <100-100- 10 = 1-P (Z «0) = 1 – $ (0) = 1-0,5 = 0,5. 356
Solución:
Por el enunciado se conoce que para este caso
es la medida de la inteligencia cuya distribución es Normal y los parámetros correspondientes son
y
.
Para realizar los calculos correspondientes importamos las bibliotecas y módulos que se necesita,
from scipy.stats import norm # Importa el submodulo asociado a la distribución normal
Entonces:
- La probabilidad que se pide está dada por
, que es equivalente a. Donde
representa la función de distribución acumulada para
. Ahora, haciendo los cálculos en Python el resultado está dado por
1 - norm.cdf(100, loc=100, scale=10) # Calcula P(X>100)
0.5
Así,
. Indicando que hay una probabilidad de 0,50 de que existan medidas de la inteligencia mayores de
.
- Se necesita calcular
, en Python es equivalente a calcular
norm.cdf(85, 100, 10) # Calcula la función de distribución para 85, P(X<85)
0.06680720126885807
Por tanto, la probabilidad de que las medidas de la inteligencia sea menor a
es igual a
- En este caso se debe calcular
norm.cdf(112, 100, 10) # Calcula la función de distribución para 112
0.8849303297782918
De esta manera la probabilidad de que las medidas de la inteligencia a lo sumo sea 112 es 0,885.
- La probabilidad requerida en este caso está dada por
, esto es lo mismo que calcular.
1 - norm.cdf(108, 100, 10)
0.21185539858339664
Así, la probabilidad de que las medidas de la inteligencia sea al menos 108 es 0,2119.
- Se debe calcular
1 - norm.cdf(90, 100, 10)
0.8413447460685429
De este modo, la probabilidad de que las medidas de la inteligencia sea mayor de 90 es 0.8413
- Esta probabilidad está dada por
. Calculando directamente tenemos que
norm.cdf(120, 100, 10)-norm.cdf(95, 100, 10)
0.6687123293258339
Este valor también se puede obtener creando dos variables y aplicando las operaciones sobre estas, es decir
a = norm.cdf(120, 100, 10) b = norm.cdf(95, 100, 10) a-b
0.6687123293258339
Entonces la probabilidad de que las medidas de la inteligencia estén entre 95 y 120 es 0,6687
Ejemplo 2.
El tiempo necesario para completar un examen de aptitud en universidades se encuentra normalmente
distribuido con media de 70 minutos y desviación estándar de 12 minutos. ¿Cuánto debe durar el examen si deseamos que 90% de los estudiantes tenga suficiente tiempo para completarlo?
Solución:
Del enunciado se puede extraer y definir que
corresponde a una variable aleatoria sobre el tiempo necesario para completar un examen de aptitud en universidades, se distribuye normal y sus parámetros son
y
.
Se pide encontrar el valor de
para el cual el 90% (0.90) de los estudiantes tienen el tiempo necesario para completar un examen de aptitud.
Esto lo podemos traducir en términos de la función de distribución de probabilidad acumulada
Por otro lado, en los métodos del submódulo norm encontramos la función de punto porcentual ppf (inversa de la función de distribución de probabilidad acumulada) que al colocar la probabilidad o cuartil (q), la media y la desviación estándar devuelve el valor de la variable aleatoria para el cual la función de distribución acumulada resulta el valor q.
Entonces,
norm.ppf(0.90, 70, 12)
85.3786187865352
Por tanto, el examen debe durar al menos 85,37 minutos para que el 90% de los estudiantes tenga tiempo suficiente para completarlo.
Ejemplo 3: generando números aleatorios provenientes de una distribución exponencial.
Lo siguiente muestra un número aleatorio (size=1) que proviene de una distribución normal con parámetros media (loc) igual a 0 y desviación estándar (scale) igual a 1.
norm.rvs(loc=0, scale=1, size=1, random_state=None)
array([0.78737108])
random_state por defecto tiene asignado el valor None pero si deseamos obtener los mismos números aleatorios cada vez que ejecutamos las líneas de código se puede asignar un número entero que corresponde a la semilla.
Nota: Se fijará la semilla para los siguientes ejemplos, esto te permitirá obtener los mismos resultados que los mostrados.
Para generar una muestra de 10 números aleatorios que provienen de una distribución normal con parámetros
y
ejecutamos una línea de código similar a la anterior, esto es
norm.rvs(loc=0, scale=1, size=10, random_state=256)
array([ 0.10430293, -0.55011253, -0.07271465, -0.35510338, -0.53282152,
-0.14452313, -0.47580717, 1.20718903, 1.37142228, -0.67320658])
O se puede ejecutar lo siguiente teniendo en cuenta que los paramétros predeterminados para la distribución son 𝜇=0 y 𝜎=1
norm.rvs(size=10, random_state=256)
array([ 0.10430293, -0.55011253, -0.07271465, -0.35510338, -0.53282152,
-0.14452313, -0.47580717, 1.20718903, 1.37142228, -0.67320658])
10 números aleatorios para una distribución Normal
y
norm.rvs(size=10, loc=23, scale=1, random_state=256)
array([23.10430293, 22.44988747, 22.92728535, 22.64489662, 22.46717848,
22.85547687, 22.52419283, 24.20718903, 24.37142228, 22.32679342])
Graficando la Distribución Exponencial
Se utilizará en este caso la biblioteca matplotlib.
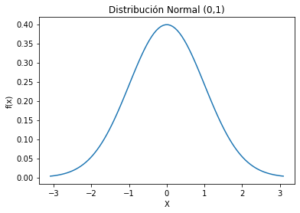
import numpy as np from scipy.stats import norm import matplotlib.pyplot as plt # Devuelve 100 valores sobre el intervalo [0.001, 0.999] x = np.linspace(norm.ppf(0.001), norm.ppf(0.999), 100) # Calcula los valores de la función de densidad de probailidad para x y = norm.pdf(x) plt.plot(x, y) # Crea el objeto gráfico plt.title('Distribución Normal (0,1)') # Título del gráfico plt.ylabel('f(x)') # Título del eje y plt.xlabel('X') # Título del eje x plt.show() # Muestra el gráfico
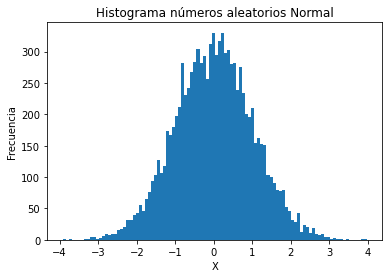
Elaborando un histograma de números Aleatorios Normal
normalrv = norm.rvs(size=10000, random_state=256) # Genera números aleatorios cuenta, cajas, ignorar = plt.hist(normalrv, 100) plt.ylabel('Frecuencia') plt.xlabel('X') plt.title('Histograma números aleatorios Normal') plt.show()
De esta distribución puedes encontrar mucha información, es una de las más utilizadas ya que muchos modelos estadísticos tienen fundamentación en esta.
Es importante que sepas que los datos no siempre siguen su comportamiento y hay distribuciones alternativas. Este artículo hizo un recorrido bastante teórico, espero te sirva de ayuda o referencia para que tengas una noción sobre está distribución.
Referencias
- Sowey, E., & Petocz, P. (2017). A Panorama of Statistics: Perspectives, Puzzles and Paradoxes in Statistics. Wiley.
- Ortega, J, & Wschebor, M.(1987). Introducción a la probabilidad. Universidad Nacional Abierta (Venezuela).
- Wackerly, S. R., & Mendenhall, W. (2009). Estadística matemática con aplicaciones. 7e. Cengage Learning Editores S.A. de C.V.
